بحث وشرح درس القيم القصوى ومتوسط معدل التغير ثالث ثانوي الفصل الاول وحل اسئلة كتاب التمارين وتحقق من فهمك وتحميل الملزمة واوراق العمل رياضيات ثالث ثانوي الفصل الدراسي الاول وفيديوهات افضل المعلمين على يوتيوب.

القيم القصوى ومتوسط معدل التغير ثالث ثانوي الفصل الاول الدرس 4-1
بحث و شرح درس
القيم القصوى ومتوسط معدل التغير
ثالث ثانوي رياضيات الفصل الاول وحل اهم اسئلة كتاب
التمارين وتحقق من فهمك. وتحميل الملزمة واوراق العمل رياضيات ثالث ثانوي الفصل الاول.
وفيديوهات افضل المعلمين على يوتيوب.
رياضيات ثالث ثانوي الفصل الاول
يمكنك تصفح جميع دروس ثالث ثانوي الفصل الاول عن طريق الرابط التالي
رياضيات ثالث ثانوي الفصل الاول اشرحلي
ملخص درس القيم القصوى ومتوسط معدل التغير.
-
التزايد والتناقص
يمكن للدوال ان ننزايد قيمتها بتزايد قيمة x او العكس ويمكن ايضا ان تظل ثابتة. فالتزايد والتناقص احدى خواص الدوال التي تساعد على فهمها ودراستها.
-
النقاط الحرجة للدالة
النقاط الحرجة للدالة هي النقاط التي تكون عندها ميل المماس للمنحنى يساوي صفرا او غير معرف.
يمكنك ايضا الاطلاع على مزيد من المعلومات عن النقاط الحرجة للدالة من خلال الويكيبيديا النقاط الحرجة للدالة ويكيبيديا -
القيم القصوى المحلية والمطلقة
القيم القصوى هي القيم العظمى او الصغرى لدالة فاذا كانت مطلقة فهي قيم قصوى في مجال الدالة كله وان كانت محلية فهي في جزء من مجال الدالة
يمكنك ايضا الاطلاع على مزيد من المعلومات عن القيم القصوى المحلية والمطلقة من خلال الويكيبيديا القيم القصوى المحلية والمطلقة ويكيبيديا -
متوسط معدل التغير
متوسط معدل التغير هو ميل المستقيم الذي يقطع المنحنى في النقطتين المراد ايجاد متوسط معدل التغير عندهم.
يمكنك ايضا الاطلاع على مزيد من المعلومات عن نظرية القيمة المتوسطة من خلال الويكيبيديا متوسط معدل التغير ويكيبيديا
تعريف درس القيم القصوى ومتوسط معدل التغير
درس القيم القصوى ومتوسط معدل التغير هو اول تطبيق على دراسة التفاضل حيث تتمكن من ايجاد النقاط التي يكون عندها قيم عظمى او قيم صغرى من خلال ايجاد النقاط الحرجة. ثم تمهيد لدراسة معدل التغير من خلال دراسة متوسط معدل التغير.
شرح درس القيم القصوى ومتوسط معدل التغير
في بداية الدرس تتعرف على مفهوم تزايد وتناقص وثبوت الدالة حيث تكون الدالة متزايدة اذا كانت قيمتها تزداد
بازدياد قيمة x وتكون متناقصة متناقصة اذا كانت تقل قيمة الدالة بنقصان قيمة x وتكون ثابتة اذا كانت قيمة
الدالة ثابتة بتغير قيمة x. ثم بعد ذلك نتعلم عن النقاط الحرجة وهي النقاط التي يكون عندها قيم قصوى حيث ان
تلك النقاط يغير المنحنى عندها سلوكه. ثم ملحوظة سريعة عن متوسط معدل التغير وهو ميل المستقيم الذي يقطع
المنحنى في النقطتين الذي يراد ايجاد متوسط معدل التغير عندهما.
يمكنك الاطلاع على شرح افضل من خلال مشاهدة الفيديوهات الموجودة بالاسفل على قناة اشرحلي او معلمين اخرين
وايضا يمكنك قراءة بحث عن الدرس اسفل الفيديوهات.
القيم القصوى ومتوسط معدل التغير يوتيوب.
نقدم لك افضل فيديوهات شرح درس القيم القصوى ومتوسط معدل التغير للمعلمين على اليوتيوب. وايضا حل اسئلة كتاب التمارين وتحقق من فهمك وتاكد.
-
القيم القصوى ومتوسط معدل التغير رياضياتي
يمكنك مشاهدة درس القيم القصوى ومتوسط معدل التغير من خلال قناة رياضياتي من خلال الفيديو التالي
-
القيم القصوى ومتوسط معدل التغير واضح
يمكنك مشاهدة درس القيم القصوى ومتوسط معدل التغير من خلال قناة واضح من خلال الفيديو التالي
-
القيم القصوى ومتوسط معدل التغير شبكة الرياضيات التعليميه
يمكنك مشاهدة فيديوهات شرح درس القيم القصوى ومتوسط معدل التغير من خلال شبكة الرياضيات التعليمية عن طريق الرابط التالي
القيم القصوى ومتوسط معدل التغير شبكة الرياضيات التعليميه
بحث عن القيم القصوى ومتوسط معدل التغير
القيم القصوى هي احد اهم الخصائص التي يمكن استخراجها من دالة حيث تاتي اهميتها من تطبيقاتها المتعددة في الحياة. فمثلا تحقيق اقصى ربح او اعلى كفاءة او اقل خسائر كلها تطبيقات ناتجة عن القدرة على ايجاد القيم القصوى. في هذا البحث نناقش اهم مفاهيم القيم القصوى والخصائص الاخرى المتعلقة بتلك الخاصية.
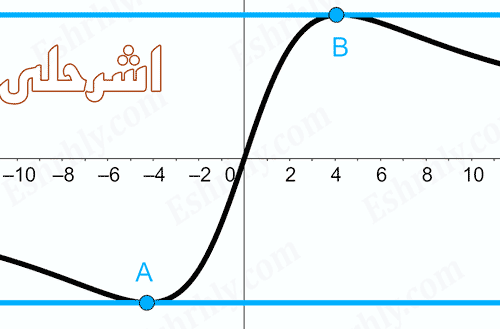
التزايد والتناقص
عند تمثيل دالة ما وبدء كتابة بعض المتغيرات في الجدول نلاحظ احيانا انه بزيادة قيمة x تزداد قيمة الدالة واحيانا بزيادة قيمة x تقل الدالة واحيانا مهما تغيرت قيمة x تظل الدالة ثابتة وتصنف الدالة تبعا لتلك الخاصية لثلاث خصائص الدالة المتزايدة، الدالة المتناقصة او الدالة الثابتة على الترتيب. نلاحظ ان منحنى الدالة يصنع زاوية موجبة مع الاتجاه الموجب من محور x اذا كانت الدالة تزايدية ومنفرجة اذا كانت الدالة تناقصية واذا كانت الدالة ثابتة فهي تمثل بمستقيم يوازي محور x.
النقاط الحرجة للدالة
هي نقاط يكون عندها قيم قصوى حيث يتغير سلوك المنحنى عندها بالنسبة للتزايد او التناقص او الثبوت. يمكن الاستدلال على تلك النقاط من خلال ايجاد النقاط التي يكون عندها ميل المماس للمنحنى مساويا للصفر او غير معرف.
القيم القصوى
تصنف القيم القصوى تبعا للمجال الذي يتم ايجادها فيه الى تصنيفين قيم قصوى مطلقة وقيم قصوى محلية. فاذا كانت القيم التي يتم ايجادها في مجال الدالة كله فان القيمة تكون قصوى مطلقة وان كانت في جزء من المجال تكون قيمة قصوى محلية. يمكن ايضا ان تكون القيم القصوى قيمة عظمى او قيمة صغرى ويتضح من المسمى ان القيمة العظمى هي اكبر وان القيمى الصغرى هي اصغر قيمة
متوسط معدل التغير
لو ان هناك سيارة تصل لمكان معين في زمن قدره ساعة واحده يمكن لتلك السيارة ان تتحرك بسرعة عالية جدا في البداية ثم تخفض سرعتها في النهاية ليكون الزمن الكلي اللازم للوصول لتلك النقطة هو ساعة واحدة. ولكن من الممكن ايضا ان تتحرك السيارة بسرعة ثابتة طوال تلك الفترة وايضا تصل لتلك النقطة في ساعة واحدة. يعبر هذا المثال عن متوسط معدل التغير فتعتبر سرعة السيارة الثابتة هي متوسط معدل التغير حيث اذا سارت العربية بسرعة ثابتة تقطع نفس المسافة في نفس الزمن التي لو كانت تحركتها بسرعة عالية ثم خفضتها.

اوراق عمل وتحضير درس القيم القصوى ومتوسط معدل التغير
يمكنك تحميل ملزمة واوراق عمل رياضيات ثالث ثانوي الفصل الاول. وأيضا ملزمة واوراق عمل وتحضير درس الاعمدة والمسافة المستقيم من خلال الرابط التالي ملزمة واوراق عمل وتحضير درس القيم القصوى ومتوسط معدل التغير


Post A Comment:
0 comments so far,add yours